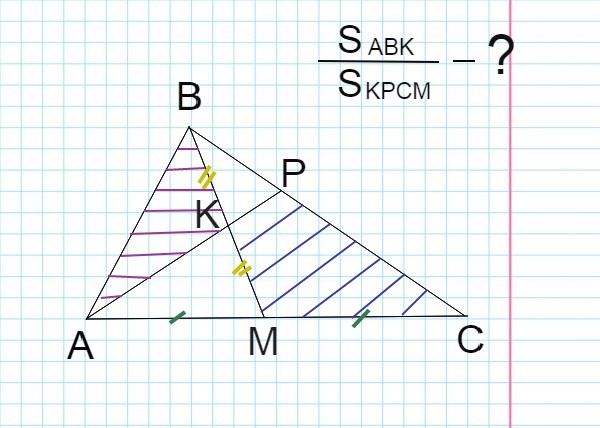
26 задание ОГЭ 2021. Геометрическая задача повышенной сложности. 9 класс.

ИзбранноеОставить комментарий

Условие: Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.

Решение:

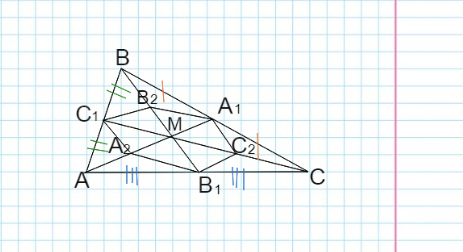
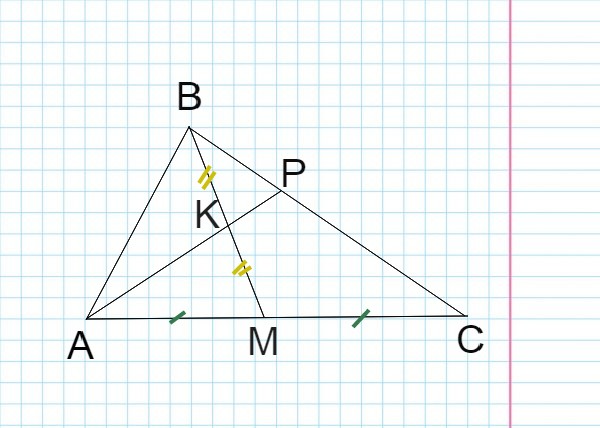
Начнем решение с выполнения чертежа к задачи.

BK = KM (по условию)

AM = MC (BM — медиана)

Обычно для решения геометрических задач повышенной сложности девятиклассникам требуется прибегнуть к дополнительному построению.

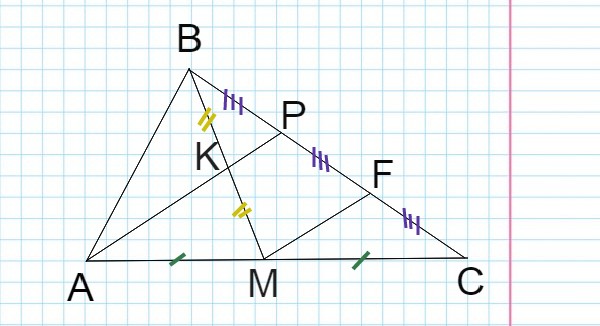
Для того чтобы перейти от площади треугольника BKP к площади треугольника BMC, а в дальнейшем и площади четырехугольника MKPC — проведем MF параллельно KP.

BP = PF (так как KP — средняя линия треугольника MBF)

FC = PF (так как KP — средняя линия треугольника APC)

Таким образом BP = PF = FC

Для удобства обозначим площадь треугольника BKP за S. Таким образом получим:

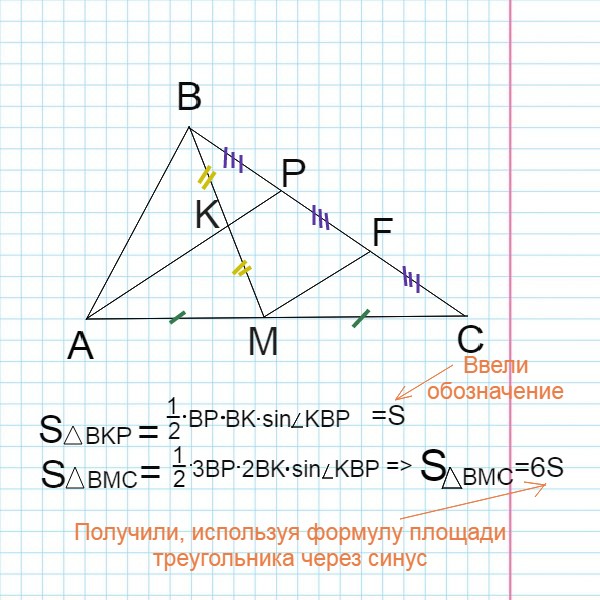
Обозначение => в математике означает «отсюда следует»

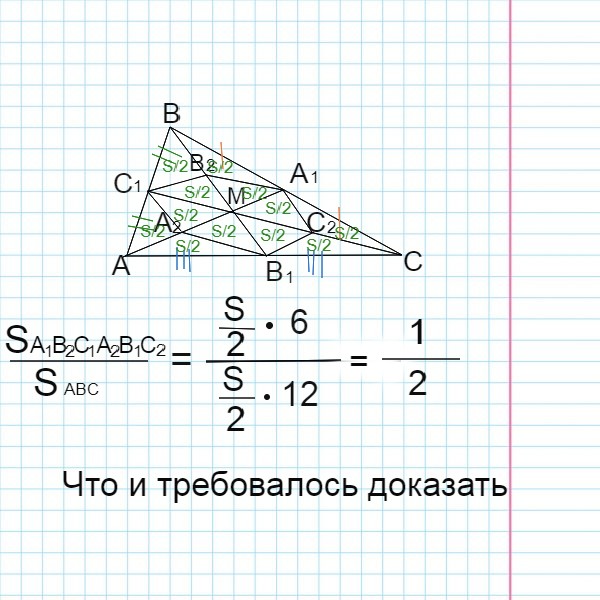
По свойству медиан треугольника: медиана разбивает треугольник на два равновеликих (равных по площади).

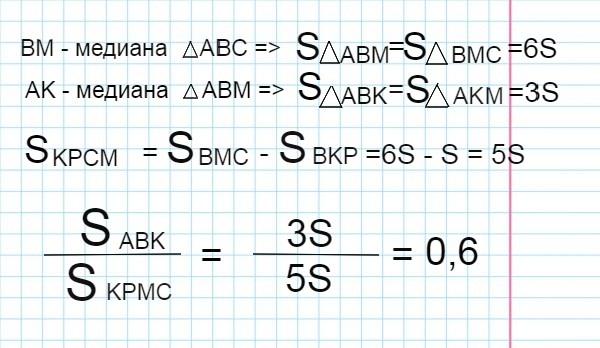
Ответ: 0,6

ЕГЭ. Профильный уровень. Планиметрическая задача

Оставить комментарий

Условие: Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Точки A2, B2 и C2 — середины отрезков MA, MB и MC соответственно.

а) Докажите, что площадь шестиугольника A1B2C1A2B1C2 вдвое меньше площади треугольника ABC.

б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что AB = 5, BC = 8 и AC = 10.

Решение:

а) Выполним чертеж и отметим равные отрезки:

AC1 = C1B ; BA1 = A1C; AB1 = B1C (так как AA1, BB1 и CC1 — медианы).

Для решения данной задачи вспомним свойства медиан треугольника:

  1. Медиана разбивает треугольник на два треугольника одинаковой площади.
  2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины.
  3. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Так как треугольник разделяется своими медиана на 6 равновеликих: S AB1M = S CB1M = S CMA1 = S BMA1 = S BMC1 = S AMC1 = S

A1B2 — медиана треугольника BMA1 из этого следует, что

S BA1B2 = S MB2A1 = S/2

Аналогично S MA1C2 = S CC2A1 = S/2; S B1MC2 = S CB1C2 = S/2;

S B1A2M = S B1AA2 = S/2; S A2AC1 = S MA2C1 = S/2;

S BB2C1 = S MB2C1 = S/2

б) AB = 5, BC = 8 и AC = 10

BA1 = A1C = 4; AB1 = B1C = 5; AC1 = C1B = 5/2

Так как AM:MA1 = 2:1 , BM:MB1 = 2:1 , CM:MC1 = 2:1 ,а точки A2, B2 и C2 — середины отрезков MA, MB и MC отсюда следует, что AA2 = A2M = MA1; BB2 = B2M = BA1; CC2 = C2M = MC1

B1C2 — средняя линия треугольника AMC и равна половина AM, то есть B1C2 =A2M.

Аналогично C1B2 — средняя линия треугольника ABM, то есть C1B2 = A2M.

C1A2 — средняя линия треугольника ABM, то есть C1A2 = B2M.

C2A1 — средняя линия треугольника BMC, то есть C2A1 = B2M.

Отметим равные отрезки:

Как видно из рисунка задача сводится к нахождению медиан треугольника.

Для дальнейшего решения воспользуемся формулой Герона и теоремой косинусов:

Ответ: 63/2